Kunci Jawaban
Kunci Jawaban Matematika Tingkat Lanjut Edisi Revisi, Kelas 11 SMA/MA: Pemahaman UK Bab 2
Inilah kunci jawaban Matematika Tingkat Lanjut kelas 11 SMA/MA: Uji Kompetensi Bab 2, halaman 94, Kurikulum Merdeka.
Penulis: Magang TribunWow
Editor: Tiffany Marantika Dewi
TRIBUNWOW.COM - Berikut ini kunci jawaban Matematika kelas 11 SMA/MA, Uji Kompetensi Bab 2: Polinomial, Halaman 94, Kurikulum Merdeka.
Buku yang ditulis Yosep Dwi Kristanto, dkk diterbitkan oleh Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi dengan nomor ISBN: ISBN 978-623-388-334-4.
Sebelum membaca artikel pada laman ini, siswa harus mengerjakan secara mandiri terlebih dahulu.
Baca juga: Kunci Jawaban Matematika Kelas 11 SMA Tingkat Lanjut Edisi Revisi: Halaman 87, Kurikulum Merdeka
Dilansir Tribunwow.com, adanya artikel ini digunakan untuk membantu orangtua dalam mengawasi dan mengoreksi hasil belajar anak.
Kunci Jawaban Uji Kompetensi Bab 2: Polinomial, Halaman 94
Kerjakan soal-soal uji kompetensi berikut ini dengan benar!
Pemahaman
Tentukan Benar atau Salah setiap pernyataan pada soal nomor 1-3
1. Perilaku ujung grafik fungsi polinomial yang berderajat ganjil dan memiliki koefisien utama negatif mengarah ke kiri bawah dan kanan atas. (↙, ↗)
Jawaban: Salah
2. Perhatikan gambar di bawah ini untuk menyimak soal nomor 2!

Hasil pembagian tersebut dapat dinyatakan sebagai berikut:
x3 - 3x - 8 = (x - 3)(x2 + 3x + 6) + 10.
Jawaban: Benar
3. Persamaan 4a2 - 1 = (2a + 1)(2a - 1) merupakan identitas polinomial.
Jawaban: Benar.
Lengkapilah pernyataan nomor 4-6 berikut dengan isian yang paling tepat.
4. Jika a ≠ 0, derajat xnym adalah
Jawaban: n + m.
5. Berdasarkan Teorema Sisa, jika polinomial P(x) dibagi dengan x + 4, sisanya adalah…
Jawaban: P(–4).
6. Derajat polinomial 9 - x + 2x2 - 4x3 - 5x4 dan 3a4b3 - 4a3 +2b3 - 10 adalah....
Jawaban: Derajatnya secara berturut-turut adalah 4 dan 7.
Jawablah pertanyaan-pertanyaan berikut ini dengan tepat
7. Deskripsikan perilaku ujung grafik polinomial F(x)= -2x3 + 3x2 + 5x - 6, kemudian pilihlah grafik pada gambar di bawah ini yang paling sesuai untuk mempresentasikan grafik fungsi f tersebut.
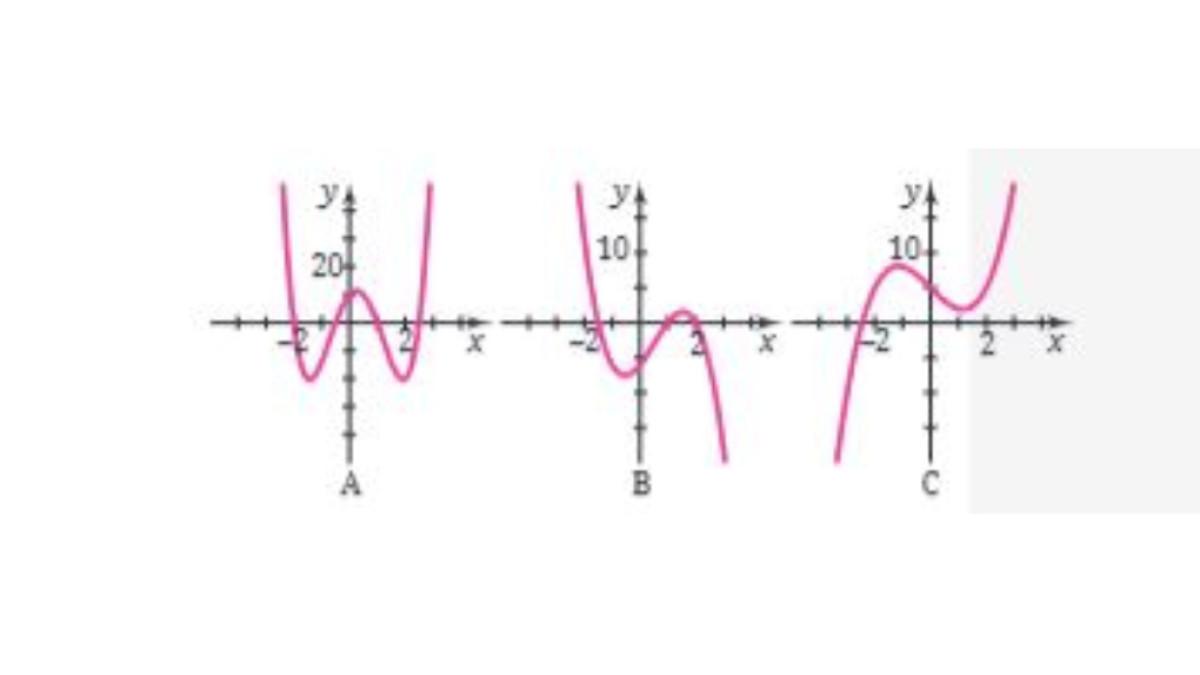
Jawaban: perilaku ujungnya ke kiri atas dan ke kanan bawah (↖, ↘) sehingga grafik B yang paling sesuai.
8. Sederhanakan (m + n + 1)(m + n - 1) - (m - n + 1)(m + n + 1).
Jawaban: 2mn – 2m + 2n2 – 2.
9. Misalkan P(x) = x4 + x3 - 3x2 - 3 dan Q(x) = (x + 2)(x - 2). Bagilah Px) dengan Q(x), kemudian nyatakan hasilnya ke dalam bentuk P(x) = Q(x) . H(x) + S(x).
Jawaban: x4 + x3 – 3x2 – 3 = (x + 2)(x – 2)(x2 + x + 1) + 4x + 1.
10. Gunakan metode Horner dan Teorema Sisa untuk menentukan nilai P(c) jika P(x) = x4 - 10x3 + 84x - 28 dan c = 9.
Jawaban: P(9) = –1.
11. Tentukan semua titik potong grafik fungsi polinomial f(x) = x3 + x2 - 5x - 5 dengan sumbu x.
Jawaban: (- √5 - , 0), (–1, 0), dan √5,0).
12. Buktikan apakah persamaan polinomial 49 - (2x + 7)2 = -2x (14 + 2x) dan (m2 + n2)2 = (m2 - n2)2 + (2mn)2 merupakan identitas polinomial.
Jawaban: Persamaan 49 – (2x + 7)2 = –2x(14 + 2x) merupakan identitas polinomial karena:
49 – (2x + 7)2 = 72 – (2x + 7)2.
= [7 – (2x + 7)][7 + (2x + 7)].
= –2x(14 + 2x).
Persamaan (m2 + n2)2 = (m2 – n2)2 + (2mn)2 juga merupakan identitas polinomial karena:
(m2 + n2)2 = m4 + 2m2n2 + n4 = (m2 – n2)2 + (2mn)2.
Penerapan
13. Luas daerah. Perhatikan daerah yang diarsir pada gambar di bawah. Daerah tersebut terletak di antara dua lingkaran yang memiliki pusat sama.
Perhatikan gambar di bawah ini untuk menjawab soal berikut
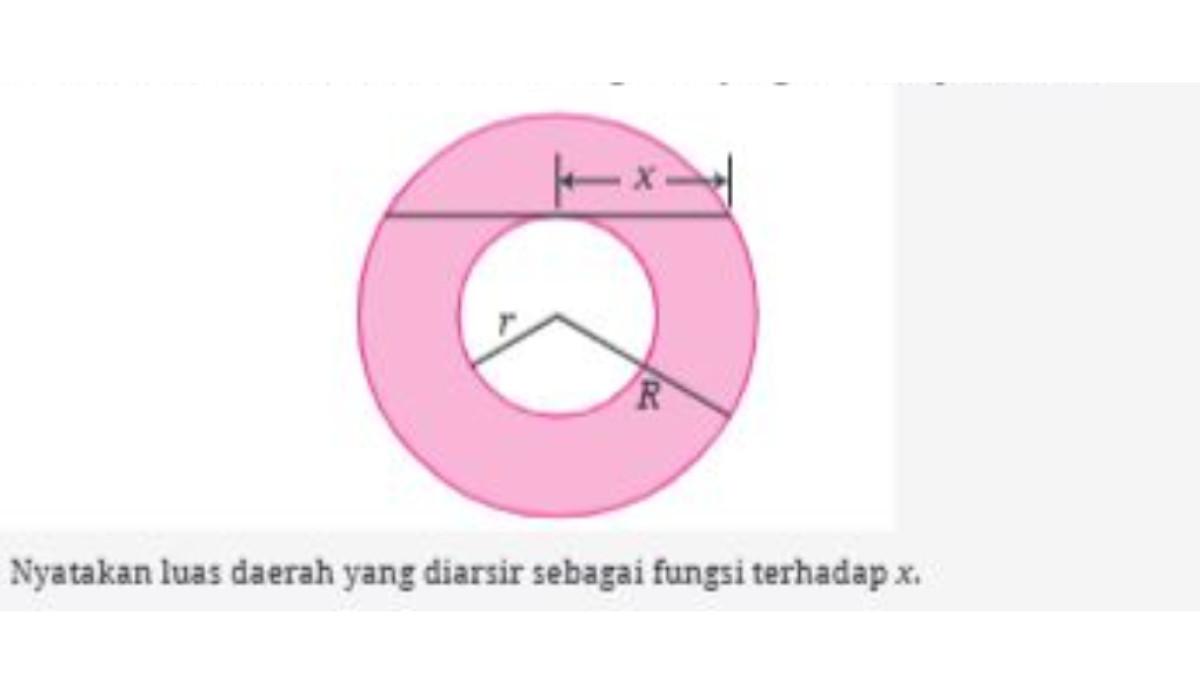
Jawaban: L = πx2.
14. Luas permukaan. Sebuah kotak karton berbentuk balok memiliki panjang, lebar, dan tinggi secara berturut-turut 50cm, 30cm, dan 25cm.
a. Tentukan luas permukaan kotak tersebut!
Jawaban: L = 7.000 cm2.
b. Jika kotak tersebut dibuat ulang dengan memotong panjang, lebar, dan tingginya sepanjang x m, tentukan luas permukaan kotak yang baru.
Jawaban: L(x) = 6x2 – 420x + 7.000.
c. Tentukan nilai x jika luas permukaan kotak yang baru adalah 3.400 m2.
Jawaban: x = 10 cm.
15. Volume. Seutas kawat sepanjang 144 cm akan digunakan untuk membuat rangka balok yang alasnya berbentuk persegi panjang dengan panjang sisi x cm.
a. Nyatakan volume balok tersebut sebagai fungsi terhadap x.
Jawaban: V(x) = 36x2 – 2x3.
b. Tentukan daerah asal fungsi pada bagian a.
Jawaban: D = {x|0 < x>
c. Tentukan volume balok tersebut untuk x = 12.
Jawbaan: 1.728 cm3.
16. Finansial. Jika uang sejumlah 100 juta rupiah ditabung ke bank selama 3 tahun, saldo uang tersebut (dalam juta rupiah) dinyatakan dalam rumus berikut.
S(x) = 100 (1 + x)3.
dengan x adalah bunga bank per tahunnya. Tentukan saldonya jikka bank tersebut memberikan bunga 5 persen per tahun.
Jawaban: Rp115.762.500,00.
17. Perhatikan soal cerita di bawah ini!
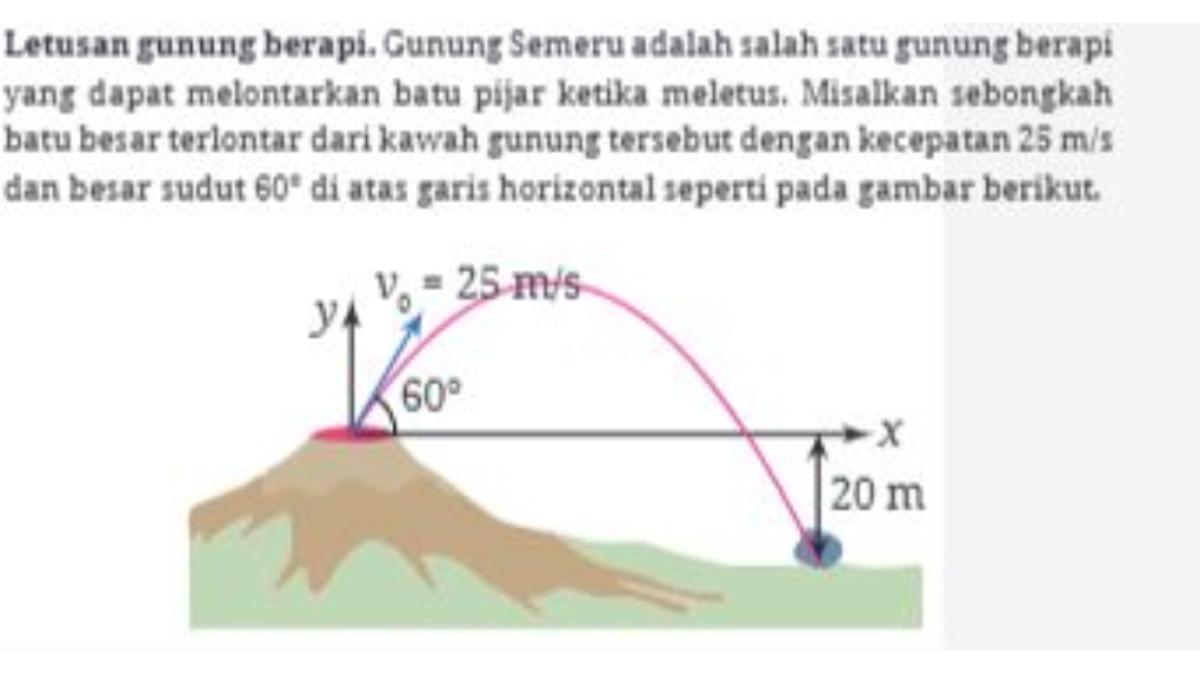
Dengan menggunakan prinsip-prinsip Fisika dan menganggap bahwa kawah gunung tersebut sebagai titik (0, 0), lintasan baru tersebut dapat dimodelkan sebagai fungsi berikut.
y = √3x - 4/125 x2.
dengan x adalah jarak horizontal yang telah ditempuh batu tersebut, sedangkan y adalah ketinggiannya relatif terhadap kawah gunung.
a. Tentukan ketinggian batu tersebut relatif terhadap kawah gunung ketika x = 25 m.
Jawaban: (25 √3 - 20 ) m atau sekitar 23,3 m.
b. Batu tersebut membentur tanah ketika terletak 20m di bawah kawah. Tentukan jarak horizontal batu tersebut dari kawah ketika sampai di tanah.
Jawaban: 25/8 (5 √3 + √139 m atau sekitar 63,9 m.
Penalaran
18. Perhatikan soal cerita dan grafik di bawah ini!
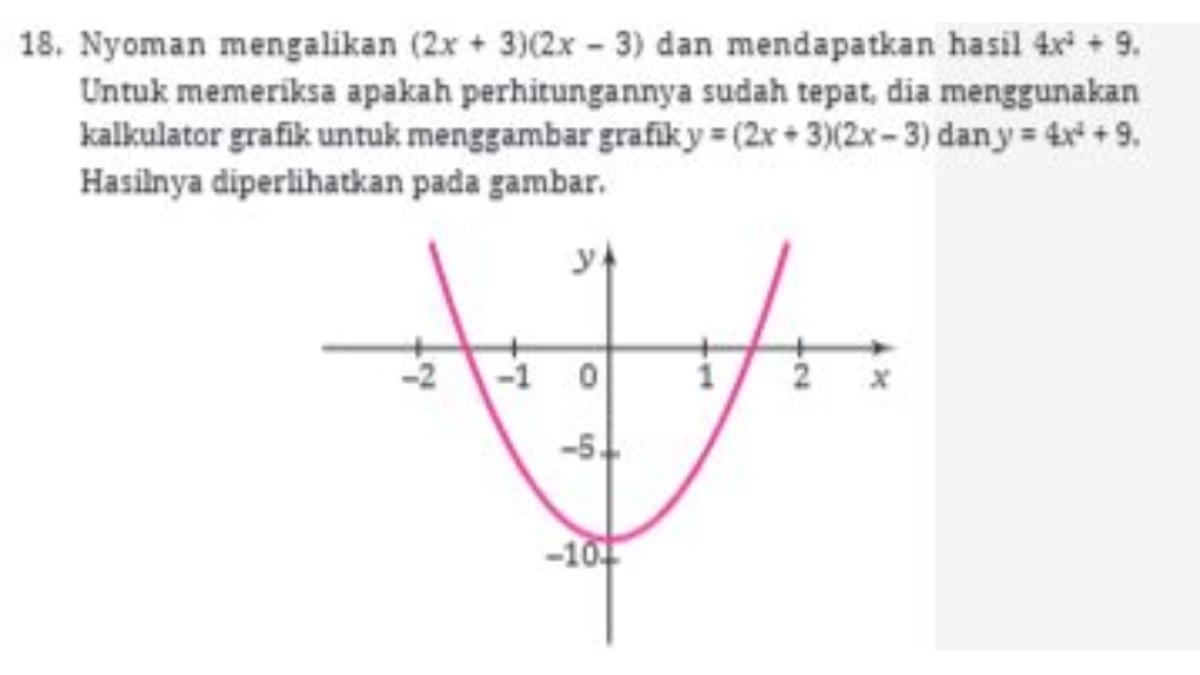
Karena hanya melihat satu grafik, dia menganggap bahwa grafik y = (2x + 3)(2x - 3) berimpit dengan grafik y = 4x2 + 9. Dengan demikian, kedua polinomial tersebut sama sehingga jawabannya sudah tepat. Jelaskan mengapa simpulan Nyoman terhadap tampilan kalkulator grafiknya tidak tepat.
Jawaban: Dengan jendela tampilan kalkulator yang dipilih, Nyoman hanya akan melihat satu grafik, yaitu grafik y = (2x + 3)(2x – 3). Akan tetapi,
ketika dia memperluas jendela tampilannya (misalnya sumbu-x diatur mulai –5 sampai 5 dan sumbu-y mulai –10 sampai 20), dia akan melihat dua grafik yang berbeda.
19. Buktikan Sifat 2,5 yaitu jika P(x) adalah polinomial yang semua koefisien dan konstantanya adalah bilangan bulat dengan koefisien utama dan konstantanya tidak nol, serta memiliki pembuat nol rasional p/q, maka p merupakan faktor dari konstanta dan q merupakan faktor dari koefisien utama P(x)).
Jawaban:
Jika p/q adalah pembuat nol rasional (dalam bentuk paling sederhana) dari polinomial P(x), maka:
an (p/q)n + an-1 (p/q)n-1 + ... + a1 (p/q) + a0 = 0.
anpn + an-1pn-1q + .... + a1pqn-1 + a0qn = 0.
p (anpn-1 + an-1pn-2q + ... + a1qn-1) = -a0qn.
Karena p adalah faktor dari bentuk ruas kiri, berarti p juga menjadi faktor dari bentuk ruas kanan. Karena p/q merupakan bentuk paling sederhana, maka p dan q tidak memiliki faktor persekutuan,
sehingga p faktor dari a0. Dengan cara yang serupa dapat ditunjukkan bahwa q merupakan faktor dari an.
*) Disclaimer
Adanya artikel ini hanya digunakan untuk memandu orang tua dalam mengawasi dan mengkoreksi hasil belajar anak.
Pastikan sebelum melihat kunci jawaban, pastikan anak sudah mengerjakannya secara mandiri terlebih dahulu.
(TribunWow.com/Peserta Magang dari Universitas Sebelas Maret/Mareta Galuh Ayuningtyas).
| Kunci Jawaban Uji kompetensi Bab 5 Pendidikan Pancasila Kelas 7 Halaman 174 Kurikulum Merdeka |

|
|---|
| Kunci Jawaban Mata Pelajaran Sejarah Kelas 10 SMK Tema Sejarah: Manusia, Ruang dan Waktu Halaman 79 |

|
|---|
| Kunci Jawaban Ilmu Pengetahuan Sosial Kelas 8 SMP/MTS, Soal Essai Uji Kompetensi Bab 2 Hal 132 |

|
|---|
| Kunci Jawaban Geografi Kelas 11 SMA/MA Bab 2 Halaman 127 Edisi Revisi Uji Kompetensi |

|
|---|
| Kunci Jawaban Ilmu Pengetahuan Sosial Kelas 8 SMP/MTS: Pilihan Ganda Uji Kompetensi Bab 2, K13 |

|
|---|




