Kunci Jawaban
Kunci Jawaban Matematika Tingkat Lanjut Edisi Revisi, Kelas 11 SMA/MA, Halaman 68, Kurikulum Merdeka
Inilah kunci jawaban Matematika Tingkat Lanjut (Edisi Revisi) kelas 11 SMA/MA, Latihan B Bab 2: Polinomial, halaman 68, Kurikulum Merdeka.
Penulis: Magang TribunWow
Editor: Tiffany Marantika Dewi
TRIBUNWOW.COM - Berikut ini kunci jawaban Matematika kelas 11 SMA/MA, Latihan B. Penjumlahan, Pengurangan, dan Perkalian Polinomial Bab 2: Polinomial, Halaman 68, Kurikulum Merdeka.
Buku yang ditulis Yosep Dwi Kristanto, dkk diterbitkan oleh Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi dengan nomor ISBN: ISBN 978-623-388-334-4.
Sebelum membaca artikel pada laman ini, siswa harus mengerjakan secara mandiri terlebih dahulu.
Baca juga: Kunci Jawaban Matematika Tingkat Lanjut Edisi Revisi, Kelas 11 SMA/MA: UK Bab 1, Halaman 39-43
Dilansir Tribunwow.com, adanya artikel ini digunakan untuk membantu orangtua dalam mengawasi dan mengoreksi hasil belajar anak.
Kunci Jawaban Latihan B. Penjumlahan, Pengurangan, dan Perkalian Polinomial Halaman 68
Kerjakan soal-soal berikut ini dengan benar!
Pemahaman Konsep
1. Bentuk 2x2 – 5x2 dapat diubah menjadi (2 – 5)x2 dengan menggunakan sifat …
Jawaban: Distributif.
2. Benar atau salah? Polinomial pertama dikurangi polinomial kedua sama dengan negatif dari penjumlahan kedua polinomial tersebut.
Jawaban: Salah. Karena jka kita memilih polinomial pertamanya 2x - 3 dan polimonial keduanya x + 5, operasi (2x - 3) - (x + 5) ≠ -[(2x - 3) + (x + 5)].
3. Benar atau salah? (5x – 1) – (3x – 4) = 5x – 1 – 3x – 4.
Jawaban: Salah. Karena seharusnya (5x - 1) - (3x - 4) = 5x - 1- 3x + 4.
Penerapan Konsep
4. Sederhanakan penjumlahan dan pengurangan polinomial berikut ini.
a. (3m2n + mn – 12) + (2m2n – mn2 + 7).
Jawaban: 3m2n + 2m2n - mn2 + mn - 12 + 7 = 5m2n - mn2 + mn - 5.
b. (2x4 – x3 + 4x – 12) – (x4 + 2x3 – x2 – 6).
Jawaban: 2x4 - x4 - x3 - 2x3 + x2 + 4x -12 + 6 = x4 - 3x3 + x2 + 4x - 6.
5. Gambar berikut menyajikan grafik fungsi polinomial f dan g. Berdasarkan grafik kedua fungsi tersebut, sketsalah grafik f(x) + g(x) dan f(x) – g(x).
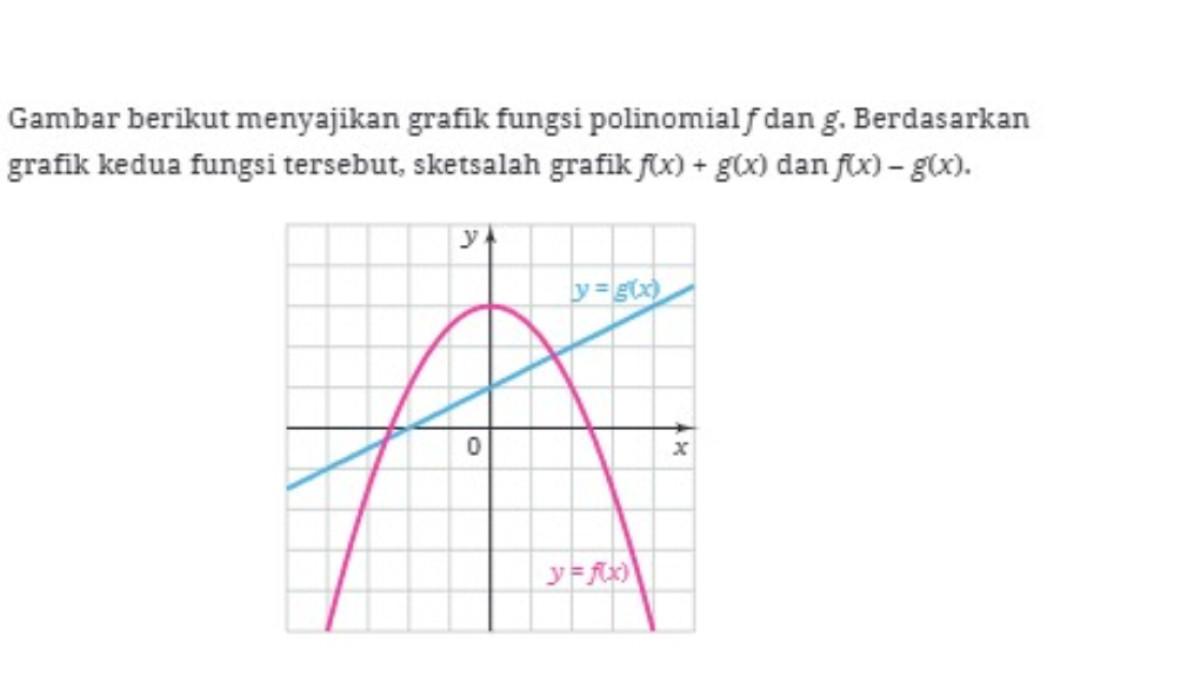
Jawaban: Berdasarkan grafik fungsi f dan g yang diketahui, grafik fungsi f(x) + g(x) dan f(x) - g(x) ditunjukkan sebagai berikut.
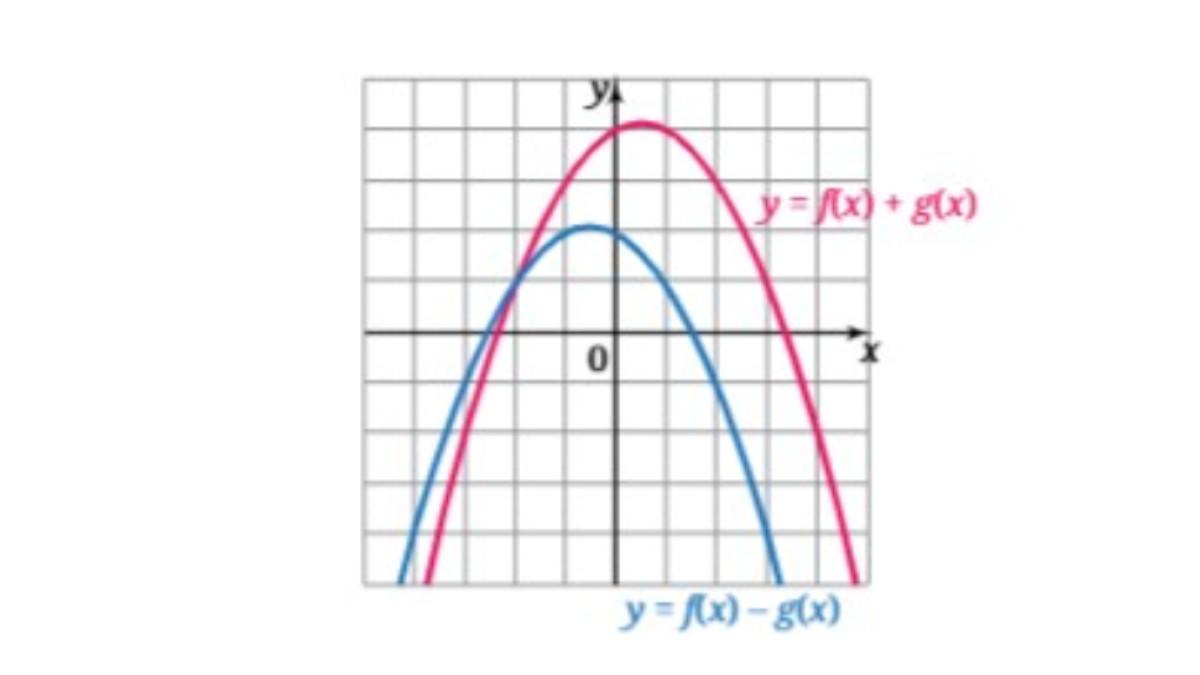
6. Tentukan hasil perkalian (3a – b + 2)(a + 2b – 5).
Jawaban: (3a - b + 2)(a + 2b - 5) = 3a2 + 5ab - 13a - 2b2 + 9b - 10.
7. Perhatikan persamaan berikut ini.

Jawaban: Tidak. Karena jika tanda kotak tersebut diganti dengan -1, persamaan A(x) = x2 - x-1 - 2 bukan merupakan polinomial.
8. Nyatakan luas daerah yang diarsir pada gambar (a) dan (b) ke dalam x.

Jawaban:
(a) Luas daerah yang diarsir dapat ditentukan dengan mengurangi luas persegi panjang besar dengan luas segitiga yang tidak diarsir.
L = [3x (x + 3)] - 1/2 [2x(x - 3)] = 2x2 + 6x.
Selain itu, luas juga dapat ditentukan menggunakan rumus luas trapesium.
L = 1/2 (x + 3)(3x + x) = 2x2 + 6x.
(b) Luas daerah yang diarsir dapat ditentukan dengan mengurangi luas daerah persegi besar dengan luas daerah persegi kecil.
L = (5x - 1)2 - x2 = 24x2 - 10x + 1.
9. Pak Alex akan memagari tanahnya yang berbentuk persegi panjang dengan pagar plastik pembibitan (lihat gambar di bawah). Karena terdapat tiupan angin yang kencang, pagar yang mengarah ke arah timur barat perlu dibuat lebih kuat.

Menurut perhitungannya, biaya pemagaran ke arah timur-barat adalah sebesar Rp1.500,00 per meter, sedangkan yang ke arah utara-selatan adalah Rp1.000,00 per meter.
Jika Pak Alex menyediakan anggaran Rp500.000,00 untuk keperluan pemagaran tersebut, nyatakan luas tanah yang dipagari sebagai fungsi L terhadap x.
Jawaban: Misalkan panjang pagar yang mengarah ke timur-barat adalah x dan panjang pagar yang mengarah ke utara-selatan adalah y.
Karena biaya pemagaran ke arah timur-barat adalah sebesar Rp1.500,00 per meter, sedangkan yang ke arah utara-selatan adalah Rp1.000,00 per meter,serta anggaran yang tersedia adalah Rp500.000,00, maka hubungan ini dapat dimodelkan sebagai berirkut.
2(1.500x + 1.000y) = 500.000 atau 1.500x + 1.000y = 250.000.
Dengan menyelesaikan y dalam persamaan tersebut, diperoleh hasil berikut.
y = 1/2 (500 - 3x).
Dengan demikian, fungsi luasnya dapat ditentukan sebagai berikut.
L = xy = x [1/2 (500 - 3x)] = 250x - 3/2 x2.
*) Disclaimer
Adanya artikel ini hanya digunakan untuk memandu orang tua dalam mengawasi dan mengkoreksi hasil belajar anak.
Pastikan sebelum melihat kunci jawaban, pastikan anak sudah mengerjakannya secara mandiri terlebih dahulu.
(TribunWow.com/Peserta Magang dari Universitas Sebelas Maret/Mareta Galuh Ayuningtyas).
| Kunci Jawaban IPS Kelas 8 Halaman 294 Kurikulum Merdeka Evaluasi Tema 4 |

|
|---|
| Kunci Jawaban PAI dan Budi Pekerti Kelas 9 SMP, Bab 4 Zakat dan Mal Kurikulum K13 |

|
|---|
| Kunci Jawaban Mata Pelajaran Sosiologi Kelas 12 SMA/MA Bab 2 Halaman 83 Soal Asesmen |

|
|---|
| Kunci Jawaban Bahasa Inggris English For Nusantara Kelas 9 SMP/MTs Chapter 2 Halaman 143 |

|
|---|
| Kunci Jawaban PAI dan Budi Pekerti Kelas 9 SMP/MTs Kurikulum Merdeka Bab 5 Halaman 140 |

|
|---|






