Kunci Jawaban
Kunci Jawaban Matematika SMP/MTs Kelas 9 Kurikulum Merdeka, Uji Kompetensi Bab 4 Halaman 269-276
Simak kunci jawaban Matematika SMP/MTs Kelas 9 Kurikulum Merdeka, Uji Kompetensi Bab 4 tentang "Peluang dan Pemilihan Sampel" halaman 269-276.
Penulis: Magang TribunWow
Editor: Elfan Fajar Nugroho
TRIBUNWOW.COM - Simak kunci jawaban Matematika SMP/MTs Kelas 9 Kurikulum Merdeka, Uji Kompetensi Bab 4 halaman 269-276.
Soal uji kompetensi ini terdapat pada bab 4 tentang Peluang dan Pemilihan Sampel.
Pada bab 4 yang membahas mengenai Peluang dan Pemilihan Sampel, peserta didik diharapkan mampu menentukan frekuensi harapan suatu kejadian dan memilih sampel dari suatu populasi.
Baca juga: Simak Kunci Jawaban Matematika Kelas 9 Halaman 70 Contoh 2.8 Kurikulum Merdeka
Buku Matematika Kelas 9 SMP/MTs Kurikulum Merdeka ini, merupakan karya dari Yosep Dwi Kristanto, dkk.
Kunci jawaban ini dapat digunakan orang tua atau wali untuk mengoreksi hasil belajar anak.
Sebelum melihat hasil kunci jawaban, pastikan siswa terlebih dahulu mengerjakan sendiri soal yang disiapkan.
Baca juga: Kunci Jawaban Pendidikan Pancasila untuk SMA/MA/SMK/MAK Kelas 12 Uji Kompetensi Halaman 212 213 214
Uji Kompetensi Bab 4
Benar atau Salah. Untuk soal nomor 1–3, tentukan apakah pernyataanpernyataan berikut benar atau salah.
1.Ada kejadian yang tidak memiliki anggota.
2.Tidak ada kejadian yang pasti.
3.Jika sebuah dadu dilempar undi sebanyak 60 kali, kita pasti mendapatkan mata dadu 6 sebanyak 10 kali.
Isian Singkat. Isilah bagian yang kosong di soal nomor 4–6.
4. Jika n(A) adalah banyaknya anggota kejadian A dan n(S) adalah banyaknya anggota ruang sampel, maka n(A) _____ n(S).
5. A adalah suatu kejadian dengan banyak anggota n(A) dan banyak anggota ruang sampelnya n(S), maka P(A) = _____.
6. Kejadian B peluangnya P(B). Peluang komplemen B adalah _____.
7–9 Ruang Sampel, Kejadian, dan Peluang. Daftarlah semua anggota ruang sampel dan kejadian yang diberikan, kemudian tentukan nilai
peluangnya.
7. Dalam lempar undi sebuah dadu, diperoleh mata dadu kurang dari 7.
8. Dalam pelemparan tiga koin, diperoleh maksimal satu sisi gambar.
9. Sebuah tas berisi lima kartu bernomor 1–5. Dua kartu diambil secara acak sekaligus dari tas tersebut dan diperoleh kartu yang
nomornya berjumlah 6.
10–12 Kejadian Pasti dan Mustahil. Dari kejadian-kejadian berikut, tentukan apakah kejadian pasti atau mustahil.
10. Dalam lempar undi dua dadu, diperoleh mata dadu-mata dadu yang jumlahnya 1.
11. Sebuah kotak berisi 25 bola warna merah. Satu bola diambil secara acak dan diperoleh bola warna merah.
12. Dalam pengambilan satu kartu dari seperangkat kartu remi secara acak, didapatkan kartu yang bukan kartu King.
13–14 Frekuensi Relatif. Tentukan frekuensi relatif setiap kejadian berikut.
13. Ketika melempar sebuah koin berkali-kali, hasilnya seperti berikut. Kejadiannya adalah kejadian muncul sisi gambar (G).
G, A, G, A, A, A, G, G, A, G, G, G
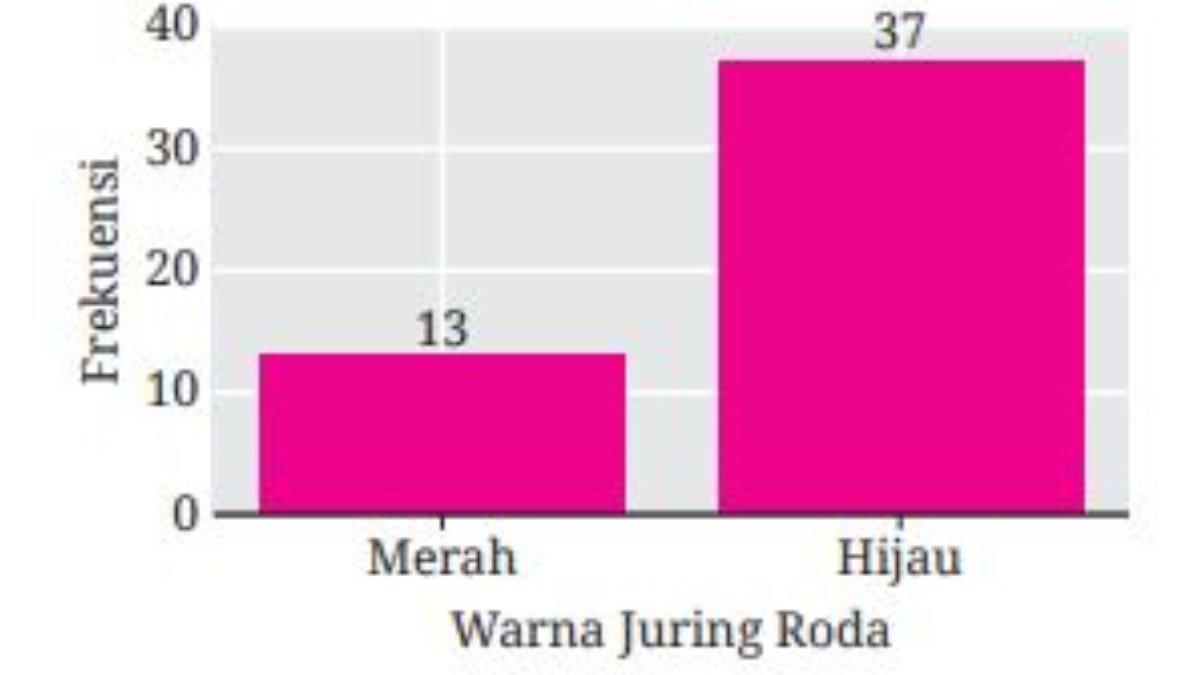
14. Gambar 4.42 menunjukkan hasil pemutaran roda yang dilakukan berulang-ulang. Kejadian yang dimaksud adalah diperolehnya
warna hijau.
15–16 Frekuensi Relatif dan Peluang Teoretis. Pasangkan diagram garis a dan b pada Gambar 4.43 dengan kejadian yang sesuai di nomor 15 dan 16. Jelaskan juga alasannya!
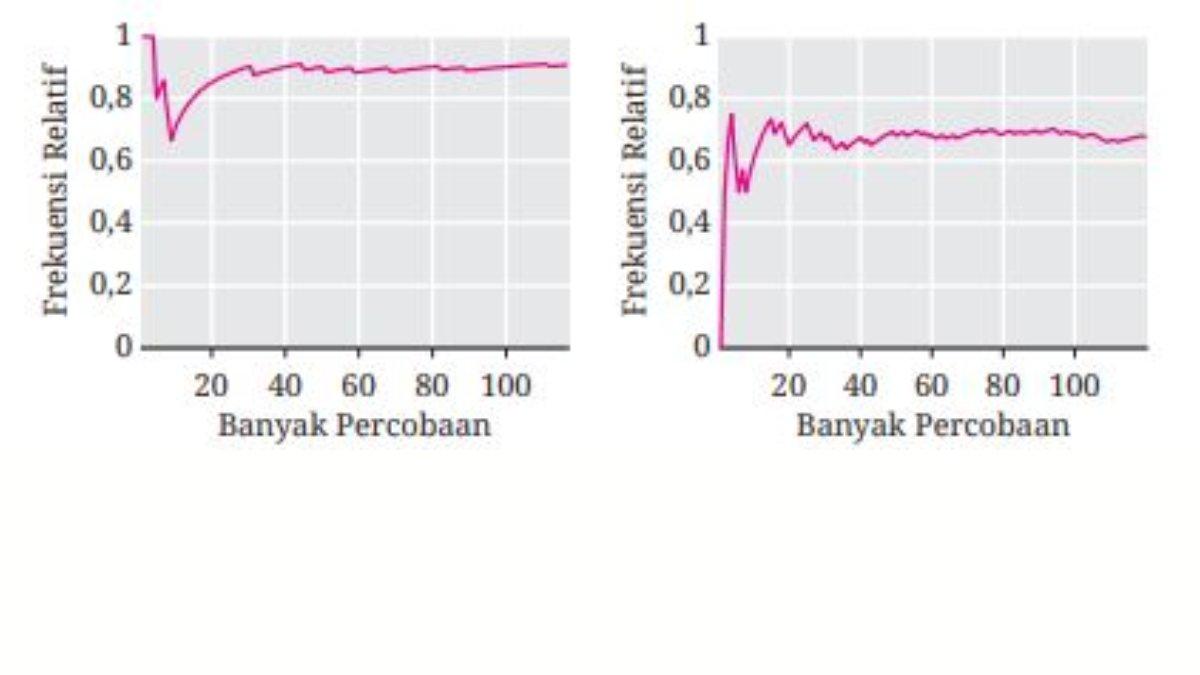
15. Dalam pemilihan satu huruf dari A sampai J, diperoleh huruf konsonan.
16. Ketika komputer diprogram untuk memilih satu bilangan mulai dari 1 sampai dengan 10, diperoleh bilangan yang tidak habis dibagi
enam.
17–18 Prediksi Ruang Sampel. Sebuah kotak terdiri dari 20 bola. setiap bola memiliki satu warna. Dugalah banyaknya bola untuk setiap
warnanya. Jelaskan alasannya
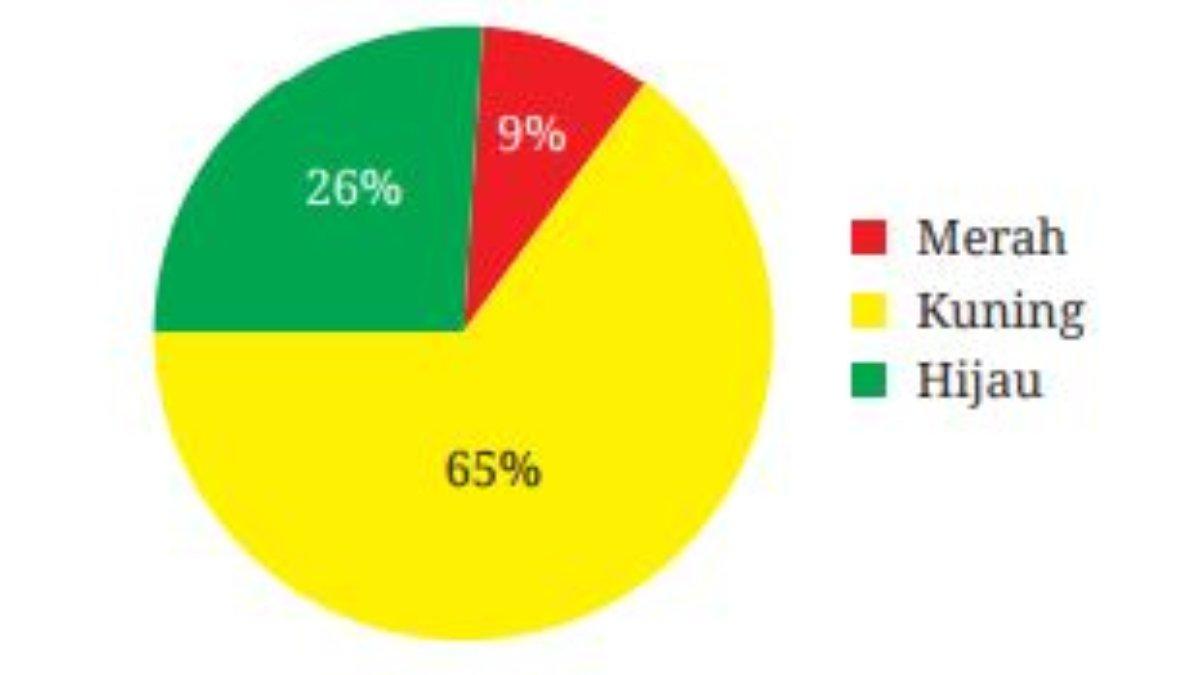
17. Setelah dilakukan percobaan yang sangat banyak, diperoleh hasil yang disajikan pada Gambar 4.44
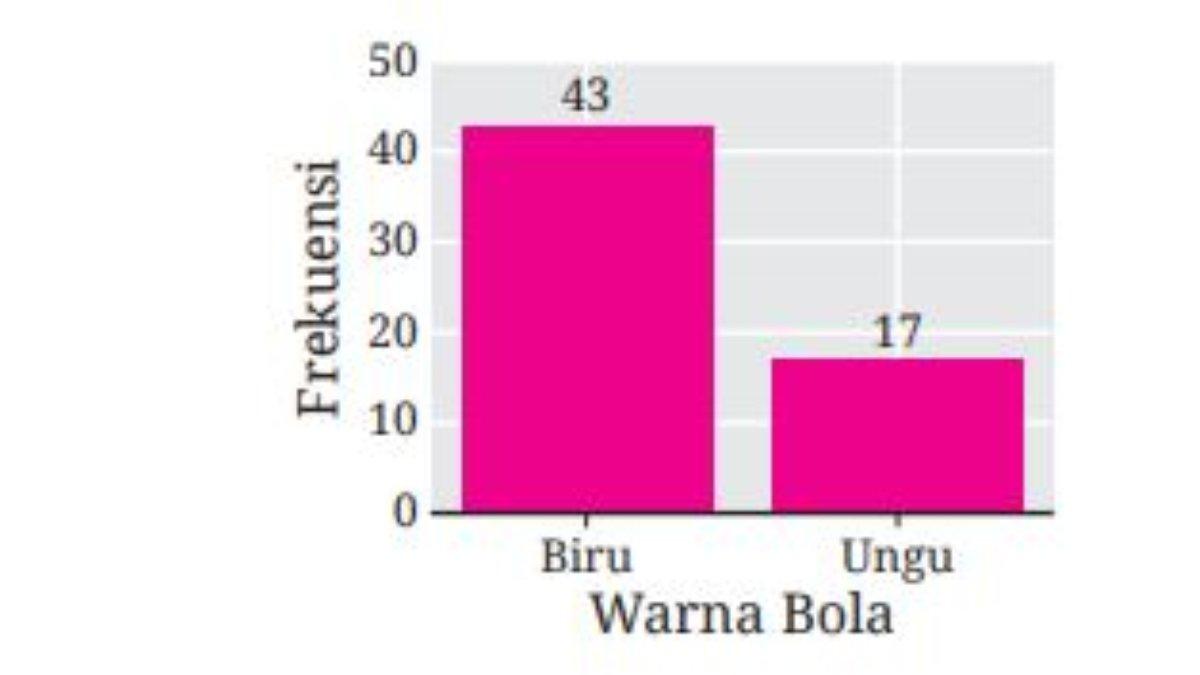
18. Gambar 4.45 menyajikan hasil percobaan beberapa kali.
19–20 Frekuensi Harapan. Tentukan frekuensi harapan setiap kejadian yang diberikan.
19. Dalam pelemparan sebuah dadu sebanyak 60 kali, diperoleh mata dadu yang kurang dari 5.
20. Sebuah roda putar terbagi menjadi delapan juring yang sama, diberi nomor 1–8. Roda tersebut diputar sebanyak 100 kali, didapatkan
bilangan prima.
21–22 Populasi dan Sampel. Tentukan populasi dan sampel yang mungkin untuk menjawab pertanyaan berikut.
21. Berapa persenkah penduduk Indonesia yang tinggal di perkotaan?
22. Pada tahun 2022, berapakah rata-rata volume sampah yang berhasil diolah oleh Bu Lestari setiap harinya?
23–24 Sampel Representatif. Untuk nomor 23 dan 24, pilihlah sampel yang representatif terhadap populasinya.
23. Gambar 4.46 menyajikan distribusi suatu populasi.
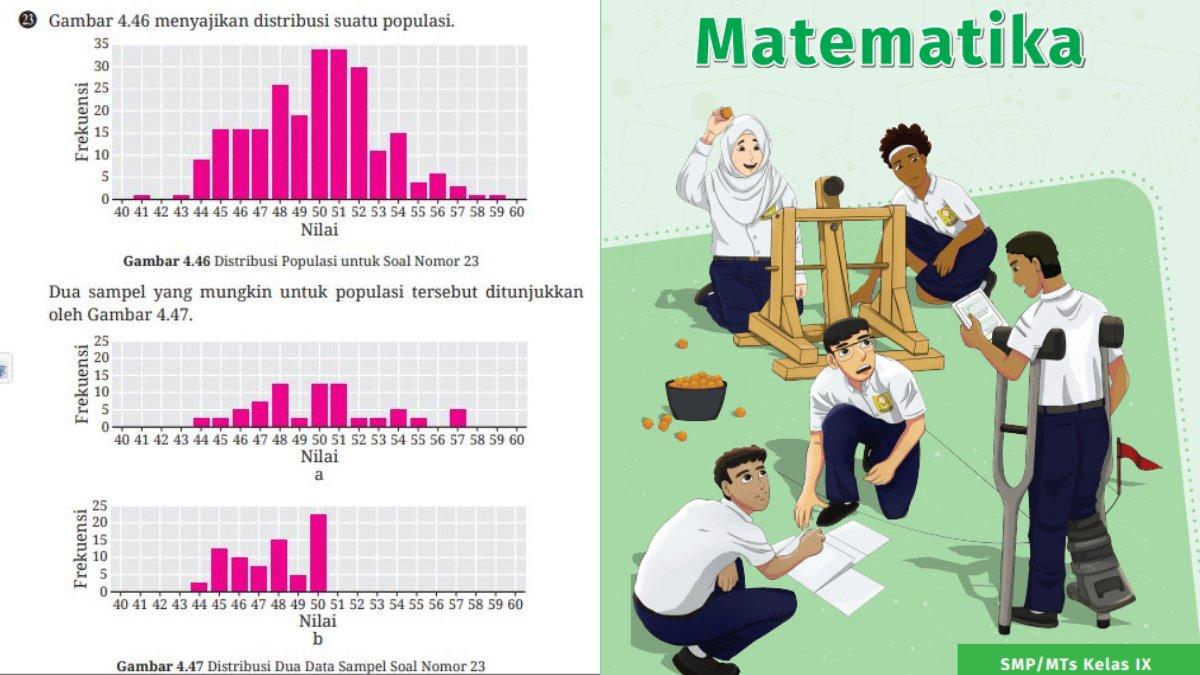
24. Distribusi dua sampel yang digambar bersamaan dengan distribusi populasinya ditunjukkan pada Gambar 4.48.
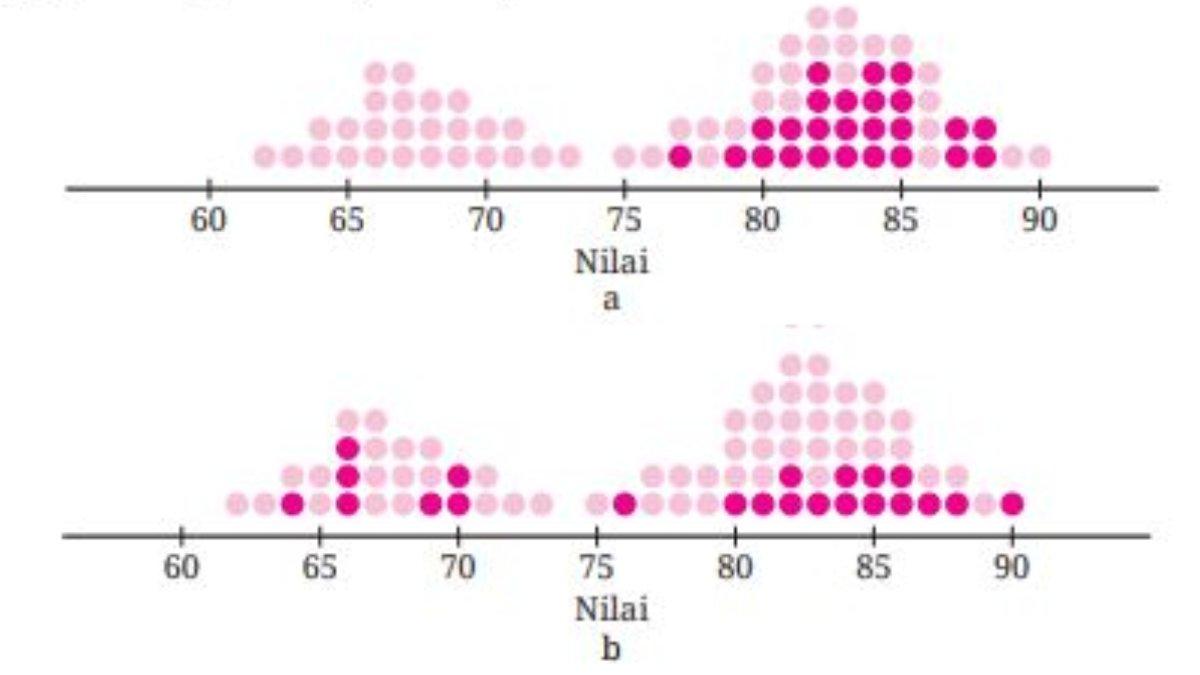
25–26 Sampel Acak. Untuk masalah-masalah di nomor 25 dan 26, carilah cara bagaimana pemilihan sampelnya agar acak.
25. Dari 27 orang siswa, seorang guru akan memilih tiga orang untuk mempresentasikan hasil pekerjaannya.
26. Karuna melakukan survei di situs jual beli ponsel bekas untuk menentukan rata-rata harganya. Dalam laman pencariannya, dia
mendapatkan 23 halaman yang masing-masing memuat 20 ponsel. Dia akan mencari sampel yang ukurannya 40.
Penerapan
27. Geografi. Pada tahun 2021, Provinsi Kepulauan Riau memiliki 364 desa/kelurahan yang letaknya di tepi laut dan 64 desa/kelurahan
bukan tepi laut. Jika kalian memilih satu desa/kelurahan di provinsi tersebut secara acak untuk dikunjungi, berapa persenkah peluang
kalian mendapatkan desa/kelurahan di tepi laut?
28. Bahan bakar. Pada tahun 2021, bahan bakar utama memasak sebagian besar rumah tangga di Nusa Tenggara Timur adalah
kayu. Perbandingan banyaknya rumah tangga yang bahan bakar memasaknya kayu dengan yang bukan kayu adalah 7 : 3. Jika kalian
berkunjung ke satu rumah tangga di provinsi tersebut secara acak, tentukan peluang kalian memperoleh rumah tangga yang bahan
bakar utama memasaknya bukan kayu.
29. Transportasi udara. Tabel 4.8 menyajikan data banyaknya penerbangan kelas ekonomi dari Medan ke Palembang pada tanggal
tertentu.
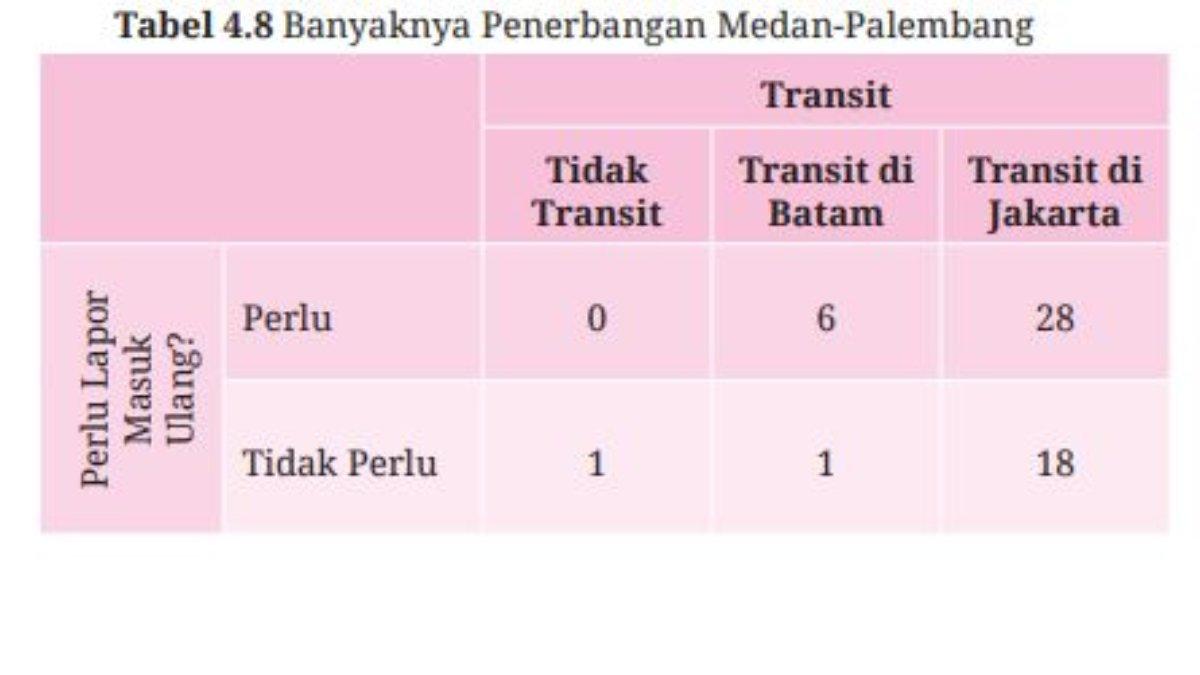
ⓐ Pada sel perpotongan antara baris “Perlu” dan kolom “Transit di Batam” berisi bilangan 6. Apa makna bilangan tersebut?
ⓑ Jika kalian memilih satu penerbangan dari Medan ke Palembang secara acak, berapakah peluang memperoleh penerbangan
yang transit di Batam?
ⓒ Dari Medan ke Palembang, Sondang ingin transit ke Jakarta. Jika dia memilih satu penerbangan secara acak yang sesuai
dengan keingingannya tersebut, berapakah peluang dia perlu lapor masuk ulang?
30. Transportasi darat. Banyaknya jenis tiket kereta api dari Bandung ke Surabaya pada tanggal tertentu ditunjukkan oleh Tabel 4.9.
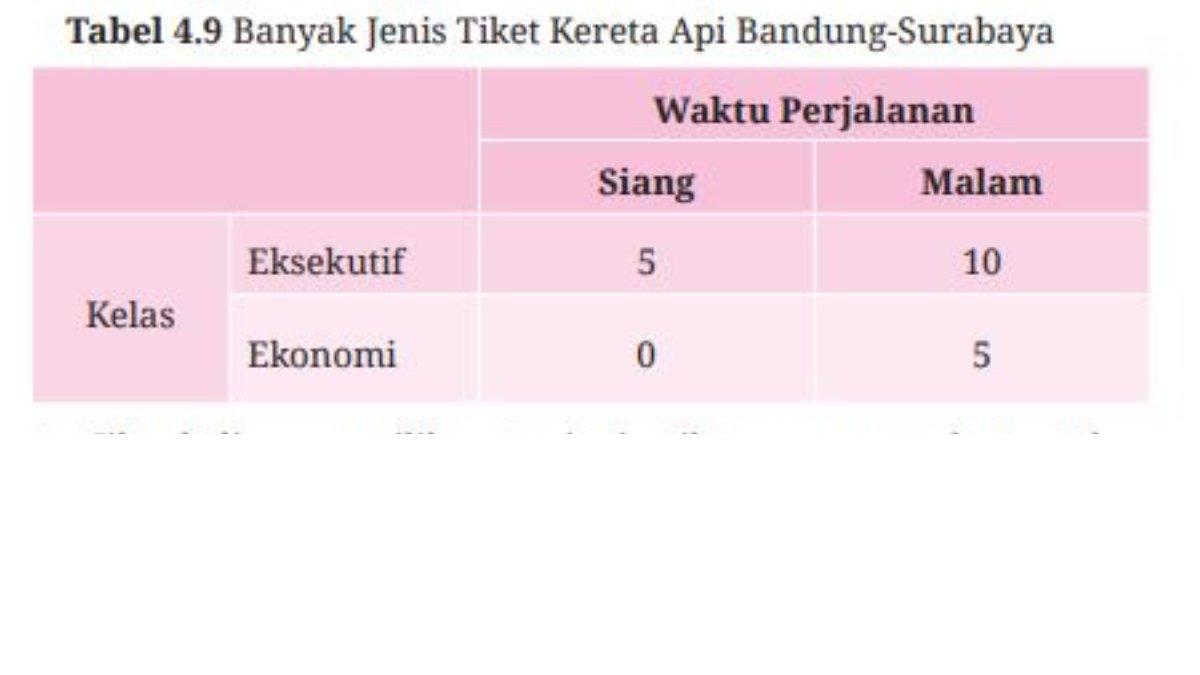
ⓐ Jika kalian memilih satu jenis tiket secara acak, tentukan peluang kalian mendapatkan tiket kereta malam.
ⓑ Carilah peluang kalian memperoleh satu jenis tiket kereta api siang kelas eksekutif jika pemilihannya secara acak.
31. Survei harga. Abel akan membeli sebuah laptop yang harganya maksimal lima juta rupiah. Untuk itu, dia melakukan percobaan
pencarian informasi harga laptop di sebuah situs web secara acak dan berulang-ulang sebanyak 20 kali. Hasilnya (dalam juta rupiah)
adalah sebagai berikut.

ⓐ Tentukan rata-rata harga laptop tersebut.
ⓑ Tentukan frekuensi relatif Abel mendapatkan laptop yang harganya sesuai dengan rencananya.
32. Golongan darah. Cermati berita dari situs resmi Ditjen Dukcapil Kementerian Dalam Negeri yang ditunjukkan Gambar 4.49.

Berdasarkan berita tersebut, tentukan frekuensi relatif penduduk yang melaporkan golongan darahnya AB.
Penalaran
33. Empat anak memiliki tinggi badan 155 cm, 140 cm, 161 cm, dan 144 cm. Jika dari empat anak tersebut dipilih tiga anak sekaligus
secara acak, tentukan peluang diperoleh anak-anak dengan ratarata tinggi badannya lebih dari 152 cm. Jelaskan alasannya!
34. Teman kalian melempar undi sebuah dadu sebanyak 5 kali. Di setiap pelemparannya, dia selalu mendapatkan mata dadu dua. Dilemparan keenam, kemungkinan besar dia akan mendapatkan mata dadu yang mana? Mengapa?
35. Kalian mengikuti sebuah kuis berhadiah. Aturan kuis tersebut adalah sebagai berikut.
• Kalian diminta oleh pewara (pembawa acara) untuk memilih satu dari tiga tirai tertutup. Salah satu tirai tersebut berisi hadiah, lainnya kosong.
• Setelah kalian memilih, pewara akan membuka satu tirai kosong yang tidak kalian pilih. Dengan demikian, tinggal dua tirai tertutup.
• Setelah itu, pewara akan memberi penawaran kepada kalian untuk berganti pilihan tirai atau tetap.
Menanggapi tawaran pewara tersebut, keputusan apa yang akan kalian pilih? Mengapa?
36. Putu adalah calon ketua kelas. Untuk mengetahui dukungan yang dia terima, dia bertanya kepada teman-teman sekelasnya sebelum
hari pemilihan. Dia berpikir bahwa dia akan mendapatkan sampel yang representatif jika dia bertanya kepada 50 persen lebih temannya. Apakah kalian setuju? Mengapa?
37. Gambar 4.50 menyajikan distribusi tiga sampel serta posisi nilai terkecil, rata-rata, dan nilai terbesar populasinya.
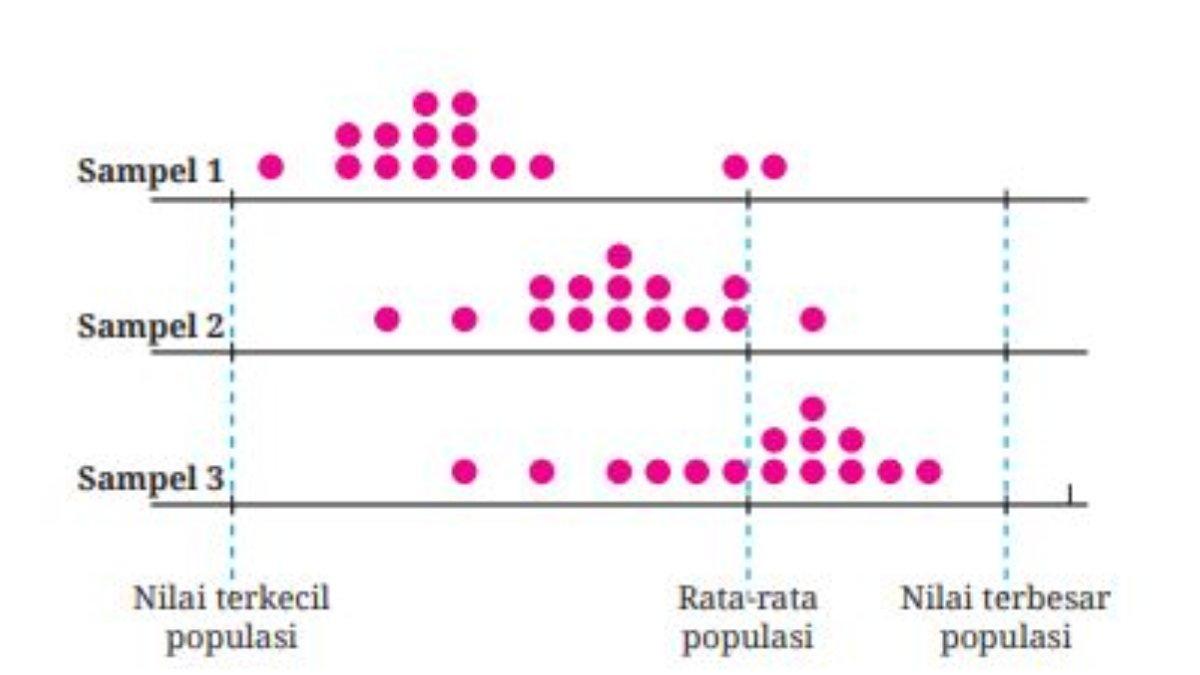
Dari ketiga sampel tersebut, manakah sampel yang representatif? Mengapa?
Jawaban
1. Benar. Kejadian tersebut adalah kejadian yang mustahil.
2. Salah. Ada kejadian yang pasti, misalnya diperolehnya mata dadu yang lebih dari 0 dalam lempar undi satu buah dadu.
3. Salah. Pemerolehan mata dadu 6 bisa kurang atau lebih dari 10 kali.
4. ≤
5. n(A)/n(S)
6. 1 – P(B)
7. S = {1, 2, 3, 4, 5, 6} dan A = {1, 2, 3, 4, 5, 6}
8. S = {(A, A, A), (A, A, G), (A, G, A), (A, G, G), (G, A, A), (G, A, G), (G, G, A), (G, G, G)} dan A = {(A, A, A), (A, A, G), (A, G, A), (G, A, A)}
9. S = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 3), (2, 4), (2, 5), (3, 1), (3, 2), (3, 4), (3, 5), (4, 1), (4, 2), (4, 3), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4)} dan A = {(1,
5), (2, 4), (4, 2), (5, 1)}
10. Kejadian mustahil karena nilai terkecil jumlah dua mata dadu adalah 2.
11. Kejadian pasti karena hanya tersedia bola merah.
12. Bukan kejadian pasti atau mustahil karena peluang kejadiannya 12/13 yang tidak sama dengan 0 ataupun 1.
13. 7/12
14. 37/50
15. Grafik b karena ujung kanan grafiknya mendekati 0,7, yaitu peluang kejadian tersebut.
16. Grafik a karena ujung kanan grafiknya mendekati 0,9, yaitu peluang kejadian tersebut.
17. 2 bola merah, 13 bola kuning, dan 5 bola hijau.
18. bola biru dan 6 bola ungu.
19. 40
20. Frekuensi harapannya adalah 50
21. Populasinya adalah seluruh penduduk Indonesia. Sampel yang mungkin di antaranya adalah (a) seluruh penduduk Indonesia yang tinggal di Jawa dan Bali; (b) seluruh penduduk Indonesia yang usianya 17 tahun ke atas; dan (c) 1000 penduduk Indonesia yang
dipilih secara acak.
22. Populasinya adalah setiap hari di tahun 2022. Sampel yang mungkin di antaranya adalah (a) setiap hari di bulan Maret 2022; (b) tanggal
25 di setiap bulan di tahun 2022; dan 40 hari di tahun 2022 yang dipilih secara acak.
23. Sampel yang representatif adalah sampel a karena distribusinya serupa dengan distribusi populasinya.
24. Sampel yang representatif adalah sampel b karena distribusinya serupa dengan distribusi populasinya.
25. Salah satunya adalah dengan menggunakan roda putar yang dibagi menjadi 27 juring yang sama, kemudian roda putar tersebut diputar
sebanyak tiga kali.
26. Salah satu caranya adalah dengan memilih dua bilangan acak dengan menggunakan komputer. Bilangan pertama merentang 1–23 yang
digunakan untuk memilih halaman dan bilangan kedua merentang 1–20 yang digunakan untuk memilih ponsel nomor berapa dalam halaman yang terpilih. Misalnya, jika Karuna mendapatkan 3 dan 17, dia perlu memilih ponsel di halaman ketiga yang urutannya ke17 di halaman tersebut. Hal tersebut dia lakukan sebanyak 40 kali.
Penerapan
27. Peluangnya 91/107 atau sekitar 0,85.
28. Peluangnya 3/10 atau 0,3.
29. a. Ada 6 penerbangan dari Medan ke Palembang di tanggal tersebut yang transit di Batam dan memerlukan lapor masuk (check-in) ulang.
b. 7/54 atau sekitar 0,13.
c. 14/23 atau sekitar 0,61
30. a. ¾ atau 0,75.
b. ¼ atau 0,25.
31. a. Rata-ratanya Rp6.343.950,00.
b. Frekuensi relatifnya 11/20.
32. Frekuensi relatifnya sekitar 0,08.
Penalaran
33. Peluangnya ¼ atau 0,25.
34. Kemungkinan besar dia akan memperoleh mata dadu dua. Ketika sebuah mata dadu dilempar undi sebanyak 5 kali dan semuanya
diperoleh mata dadu dua, kemungkinan besar dadu tersebut tidak adil. Artinya, mata dadu memiliki peluang yang lebih besar
daripada mata dadu-mata dadu lainnya.
35. Dengan berdasarkan peluang teoretik, keputusan yang perlu dipilih adalah berganti pilihan tirai. Dengan memilih tirai awal, peluang
menangnya hanya 1/3. Jika berganti tirai, peluang menangnya menjadi 2/3.\
36. Tidak setuju. Dengan bertanya kepada 50 persen lebih dari teman-teman sekelasnya, tidak ada jaminan bahwa dia akan mendapatkan sampel yang representatif. Sebagai contoh, misalnya saja dalam satu kelas yang terdiri dari 30 peserta didik, 12 (40 persen) di antaranya memilih
Putu sebagai ketua kelas. Ketika dia bertanya kepada 16 temannya, dia mungkin saja mendapatkan bahwa 11 (68,75%) di antaranya
memilihnya sebagai ketua kelas. Persentase yang diperoleh dari populasi dan sampel tersebut sangat jauh. Hal ini menunjukkan bahwa ada kemungkinan dengan menggunakan caranya, dia mendapatkan sampel yang tidak representatif.
37. Sampel yang representatif terhadap populasinya adalah sampel 3 karena distribusi data yang disajikan lebih ke kanan. Dengan
demikian, ukuran pemusatannya, yaitu rata-rata, juga akan lebih ke kanan (lebih besar).
*) Disclaimer :
Jawaban di atas hanya digunakan untuk memandu proses belajar anak.
Soal ini berupa pertanyaan terbuka yang artinya ada beberapa jawaban tidak terpaku seperti di atas.
(TribunWow.com/Peserta Magang dari Universitas Sebelas Maret/Marita Nur Isnawati)
Baca Berita Menarik Lainnya di Google News
Sumber: TribunWow.com
| Kunci Jawaban Buku PAI dan Budi Pekerti Kelas 9 SMP/MTS Kurikulum Merdeka Bab 9 Halaman 196-198 |
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/Buku-Pendidikan-Agama-Islam-Dan-Budi-Pekerti-Kelas-9-SMPMTS.jpg)
|
|---|
| Kunci Jawaban Matematika Kelas 5 SD/MI: Ayo Berlatih Bab 2, Halaman 52-53, Kurikulum Merdeka |
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/KUNCI-JAWABAN-Matematika-Kelas-5-SDMI-Ayo-Berlatih-Bab-2-Halaman-42.jpg)
|
|---|
| Kunci Jawaban Animasi Kelas 12 SMK/MAK Uji Kompetensi Bab 2 Kurikulum Merdeka Halaman 165 |
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/ANIMASI-2.jpg)
|
|---|
| Kunci Jawaban Informatika Kelas 7 SMP/MTs Bab 3 Halaman 131 Uji Kompetensi Nomor 1-8 |
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/info.jpg)
|
|---|
| Kunci Jawaban Buku PAI dan Budi Pekerti Kelas 9 SMP/MTS Kurikulum Merdeka Bab 6 Halaman 130-132 |
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/Buku-PAI-dan-Budi-Pekerti-untuk-kelas-9-SMPMTS-Kurikulum-Merdeka-Bab-6.jpg)
|
|---|
:quality(30):format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/Kunci-Jawaban-Matematika-SMP-2111.jpg)
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/info-update-cuaca.jpg)
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/rumah-ahmad-sahroni-dibongkar.jpg)
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/pramono-anungg.jpg)
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/cover-bab-2-ekonmi-kls10.jpg)
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/ilustrasi-polisi-baru.jpg)
:format(webp):focal(0.5x0.5:0.5x0.5)/wow/foto/bank/originals/PRAKIRAAN-CUACA-Foto-hujan-yang-mengguyur-area-kantor-Tribun-Network-di-Klodran-Colomadu.jpg)