Kunci Jawaban
Kunci Jawaban Matematika Kelas 11 SMA Tingkat Lanjut Edisi Revisi: Halaman 87, Kurikulum Merdeka
Inilah kunci jawaban Matematika Tingkat Lanjut (Edisi Revisi) Kelas 11 SMA/MA, Latihan D, Bab 2: Polinomial, halaman 87, Kurikulum Merdeka
Penulis: Magang TribunWow
Editor: Tiffany Marantika Dewi
TRIBUNWOW.COM - Berikut ini kunci jawaban Matematika kelas 11 SMA/MA, Latihan D. Faktor dan Pembuat Nol Polinomial, Bab 2: Polinomial, Halaman 87, Kurikulum Merdeka.
Buku yang ditulis Yosep Dwi Kristanto, dkk diterbitkan oleh Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi dengan nomor ISBN: ISBN 978-623-388-334-4.
Sebelum membaca artikel pada laman ini, siswa harus mengerjakan secara mandiri terlebih dahulu.
Baca juga: Kunci Jawaban Matematika Tingkat Lanjut Edisi Revisi, Kelas 11 SMA/MA, Halaman 68, Kurikulum Merdeka
Dilansir Tribunwow.com, adanya artikel ini digunakan untuk membantu orangtua dalam mengawasi dan mengoreksi hasil belajar anak.
Kunci Jawaban Latihan D. Faktor dan Pembuat Nol Polinomial, Halaman 87
Kerjakan soal-soal berikut ini dengan benar!
Pemahaman Konsep
1. Untuk suatu polinomial P(x), nilai P(10) adalah 0. Dengan demikian, …. adalah faktor polinomial tersebut.
Jawaban: (x – 10)
2. Benar atau salah? Grafik fungsi polinomial P(x) memotong sumbu-x di titik (3, 0). Dengan demikian, (x + 3) adalah faktor dari P(x).
Jawaban: Salah. Jika grafik fungsi polinomial P(x) memotong sumbu-x di titik (3, 0), pembuat nolnya adalah x = 3. Dengan demikian, yang menjadi faktor P(x) adalah x – 3. Bentuk x + 3 belum tentu faktor dari P(x).
3. Benar atau salah? Fungsi P(x) = (x + 7)(x + 3)(x – 2) adalah fungsi polinomial berderajat tiga satu-satunya yang grafiknya memotong sumbu-x di (–7, 0), (–3, 0), dan (2, 0).
Jawaban: Salah. Ada fungsi polinomial lainnya, misalnya Q(x) = 2(x + 7) (x + 3) (x – 2).
Penerapan Konsep
4. Jika P(x) = x4 – 2x3 – 13x2 + 14x + 24, tunjukkan bahwa P(–3) = 0 dan P(2) = 0. Gunakan fakta tersebut untuk memfaktorkan P(x) secara lengkap.
Jawaban:
P(–3) = (–3)4 – 2(–3)3 – 13(–3)2 + 14(–3) + 24.
= 81 + 54 – 117 – 42 + 24 = 0.
dan
P(2) = (2)4 – 2(2)3 – 13(2)2 + 14(2) + 24.
= 16 – 16 – 52 + 28 + 24 = 0.
Bentuk pemfaktorannya adalah (x – 4)(x – 2)(x + 1)(x + 3).
5. Faktorkan P(x) = 5x3 – 28x2 + 45x – 18 secara lengkap.
Jawaban: P(x) = (5x – 3)(x – 2)(x – 3).
6. Dari ketiga grafik pada gambar di bawah, manakah yang merupakan grafik f(x) = (x + 1)2 (x – 1)2?
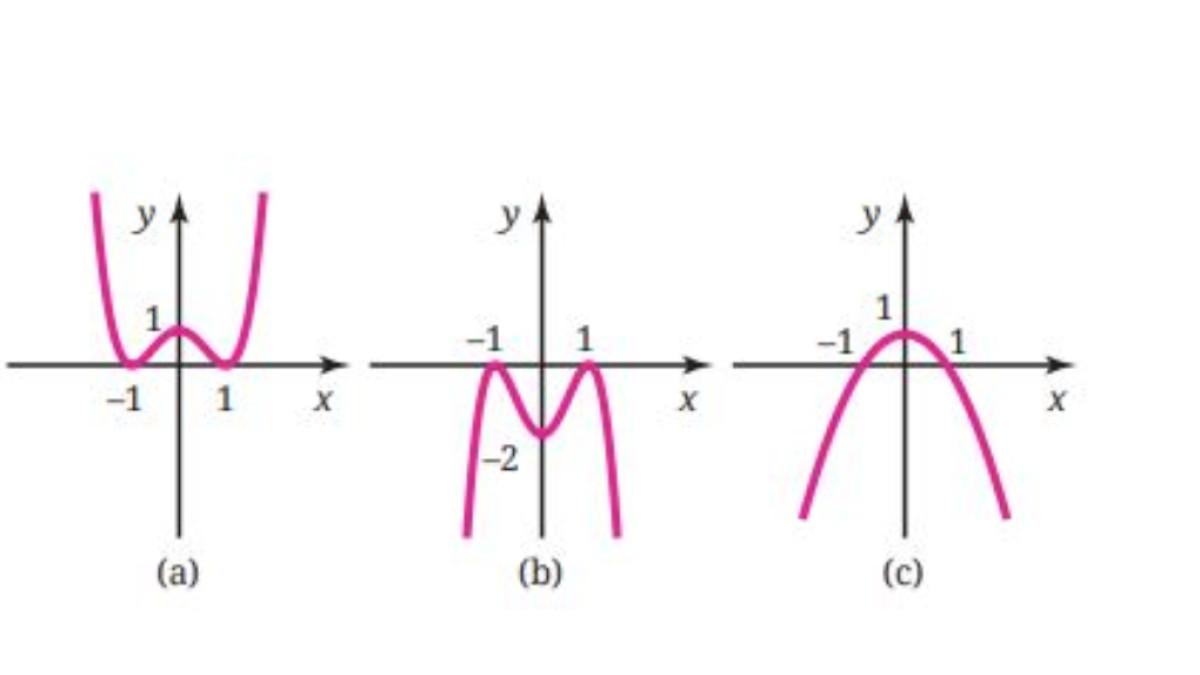
Jawaban: Grafik f(x) = (x + 1)2 (x – 1)2 memotong sumbu-x di (–1, 0) dan (1, 0). Karena f(0) = (0 + 1)2 (0 – 1)2 = 1, grafiknya memotong sumbu-y di (0, 1). Karena fungsi polinomial ini berderajat genap dan koefisien utamanya positif, perilaku ujung grafiknya ke kiri atas dan ke kanan atas (↖, ↗). Dengan demikian, grafik yang tepat adalah grafik (a).
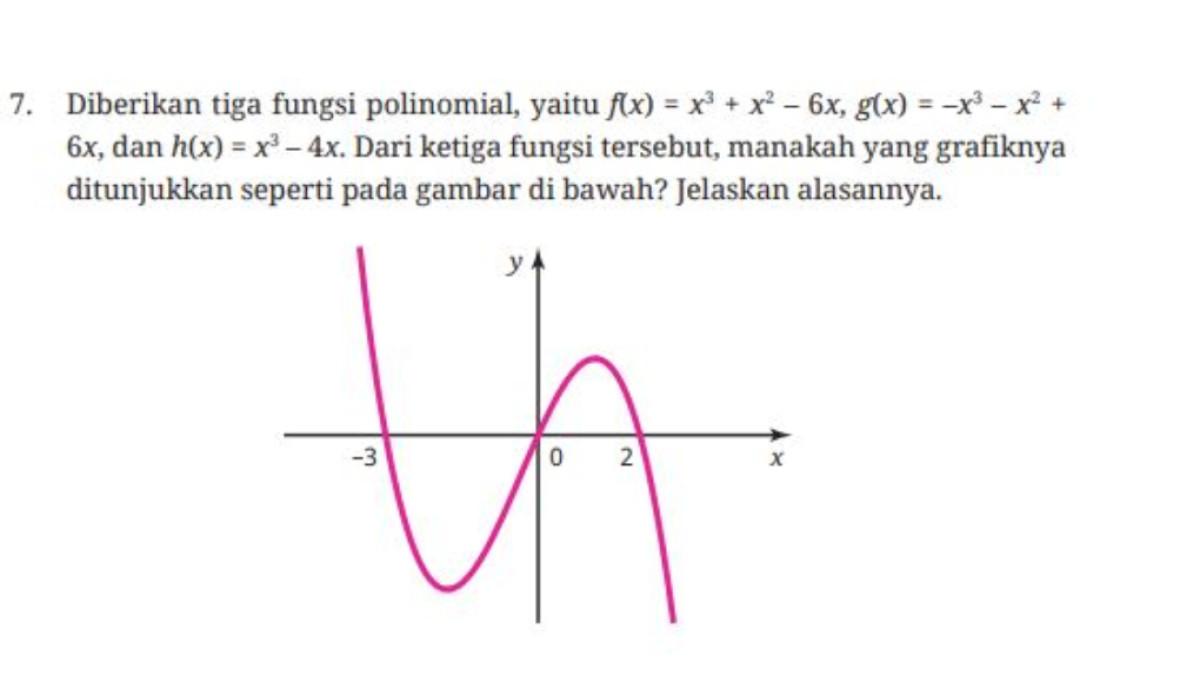
7. Diberikan tiga fungsi polinomial, yaitu f(x) = x3 + x2 – 6x, g(x) = –x3 – x2 + 6x, dan h(x) = x3 – 4x. Dari ketiga fungsi tersebut, manakah yang grafiknya ditunjukkan seperti pada gambar di bawah? Jelaskan alasannya.
Jawaban:
Dilihat dari bentuk dan perilaku ujungnya (↖, ↘), grafik yang diberikan merupakan grafik fungsi polinomial berderajat 3 dengan koefisien utama negatif. Dengan demikian, dari pilihan yang diberikan, fungsi yang paling tepat adalah g(x) = –x3 – x2 + 6x. Selain itu, karena g(x) = –x3 – x2 + 6x = –x(x + 3)(x – 2), grafik fungsi ini memotong sumbu-x di (0, 0), (–3, 0), dan (2, 0).
Hal ini juga sesuai dengan grafik yang diberikan.
8. Carilah polinomial berderajat 4 yang pembuat nolnya adalah –3, 0, 1, dan 4 dan koefisien x 2-nya adalah 11.
Jawaban:
9. Jika x + 2 dan x – 3 adalah faktor dari P(x) = 2x3 + ax2 + bx + 18, tentukan nilai a dan b.
Jawaban: Jika x + 2 dan x – 3 adalah faktor dari P(x) = 2x3 + ax2 + bx + 18, berdasarkan Teorema Faktor, P(–2) = 0 dan P(3) = 0. Dengan demikian, diperoleh sistem persamaan linear dua variabel berikut.
Simak gambar di bawah ini untuk informasi selengkapnya!

10. Sebuah peti kemas memiliki panjang 1 meter lebih dari dua kali lebarnya, sedangkan tingginya dua kali lebarnya. Jika volume peti kemas tersebut 936 m3, tentukan luas permukaan peti kemas tersebut.
Jawaban:
Diketahui sebuah peti kemas memiliki panjang 1 meter lebih dari dua kali lebarnya, sedangkan tingginya dua kali lebarnya. Volume peti kemas tersebut 936 m3. Misalkan l adalah lebar peti kemas tersebut, informasi tersebut dapat dimodelkan sebagai berikut.
(2l + 1)l(2l) = 936.
*) Disclaimer
Adanya artikel ini hanya digunakan untuk memandu orang tua dalam mengawasi dan mengkoreksi hasil belajar anak.
Pastikan sebelum melihat kunci jawaban, pastikan anak sudah mengerjakannya secara mandiri terlebih dahulu.
(TribunWow.com/Peserta Magang dari Universitas Sebelas Maret/Mareta Galuh Ayuningtyas)
| Kunci Jawaban Mata Pelajaran Informatika Kelas 9 SMP/MTs Bab 3 Halaman 63 Uji Kompetensi Uraian |

|
|---|
| Kunci Jawaban Mata Pelajaran Pendidikan Pancasila Kelas 6 SD/MI Bab 3 Halaman 73 Ayo, Kamu Bisa |

|
|---|
| Kunci Jawaban Matematika Tingkat Lanjut Edisi Revisi, Kelas 11 SMA/MA, Halaman 68, Kurikulum Merdeka |

|
|---|
| Kunci Jawaban IPS Kelas 8 Halaman 294 Kurikulum Merdeka Evaluasi Tema 4 |

|
|---|
| Kunci Jawaban PAI dan Budi Pekerti Kelas 9 SMP, Bab 4 Zakat dan Mal Kurikulum K13 |

|
|---|